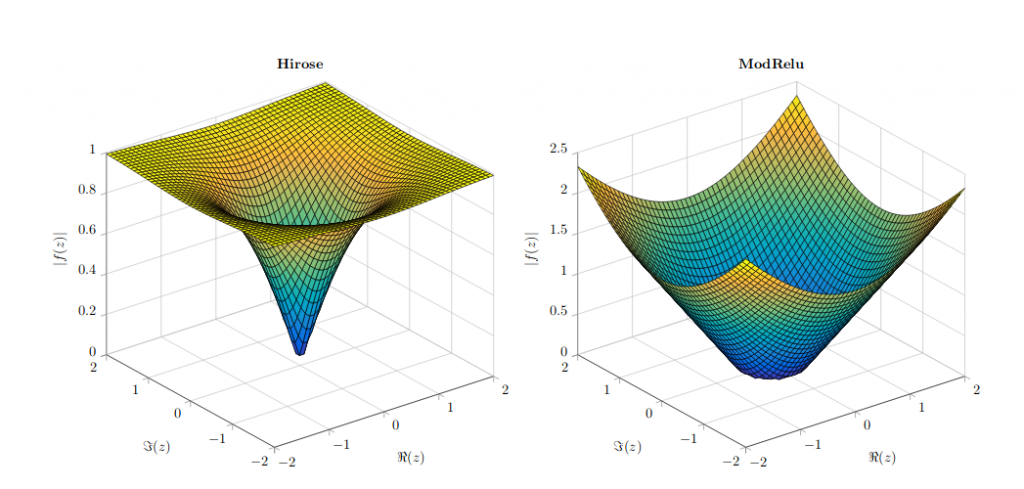
The paper Complex gated recurrent neural networks explores machine learning in the complex domain. For gradient descent to work the functions involved must be differentiable. In the complex domain holomorphic functions, which satisfy the Cauchy-Riemann partial differential equations are differentiable. Finding functions which fulfill this requirement and are useful for machine learning tasks is very difficult. In practice split differentiable complex functions are used which are real differentiable in the real and complex parts. This is true for the two most popular complex activation functions the ModRelu and the Hirose non-linearites shown below:
Modern RNNs rely on gating equations for memory management. Typically the gates produce values between zero and one, where one means that a value will be stored in the memory cell and zero that it will be removed. In the complex domain this behavior can be reproduced by using mappings from C to R, in particular a weighted average of the real and imaginary parts can be fed into a sigmoid non-linearity.
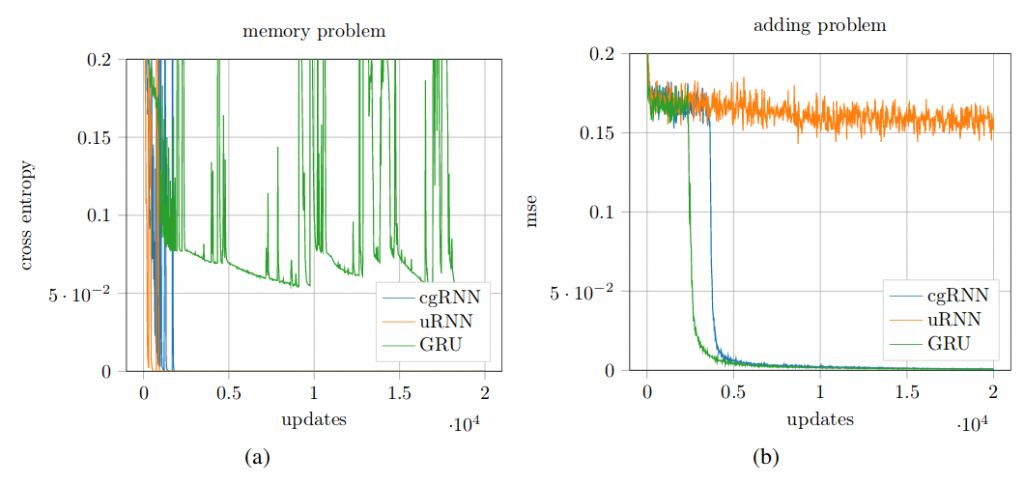
Using the split differentiable approach with a hirose activation and C to R gates its possible to define complex memory cells. The plot below tests their performance on the synthetic memory and adding benchmark problems.
In short it can be observed that the complex gated cell can solve both the memory as well as the adding problem, when it combines the complex orthogonal structures from uRNNs with a gating mechanism similar to classic RNNs. For a more detailed discussion please take a look at the full paper
Below a complex memory unit solving the human motion prediction problem can be seen in action:
The code for this project is available on Github. I tested the complex memory cell on human motion data using a setting following this repository.